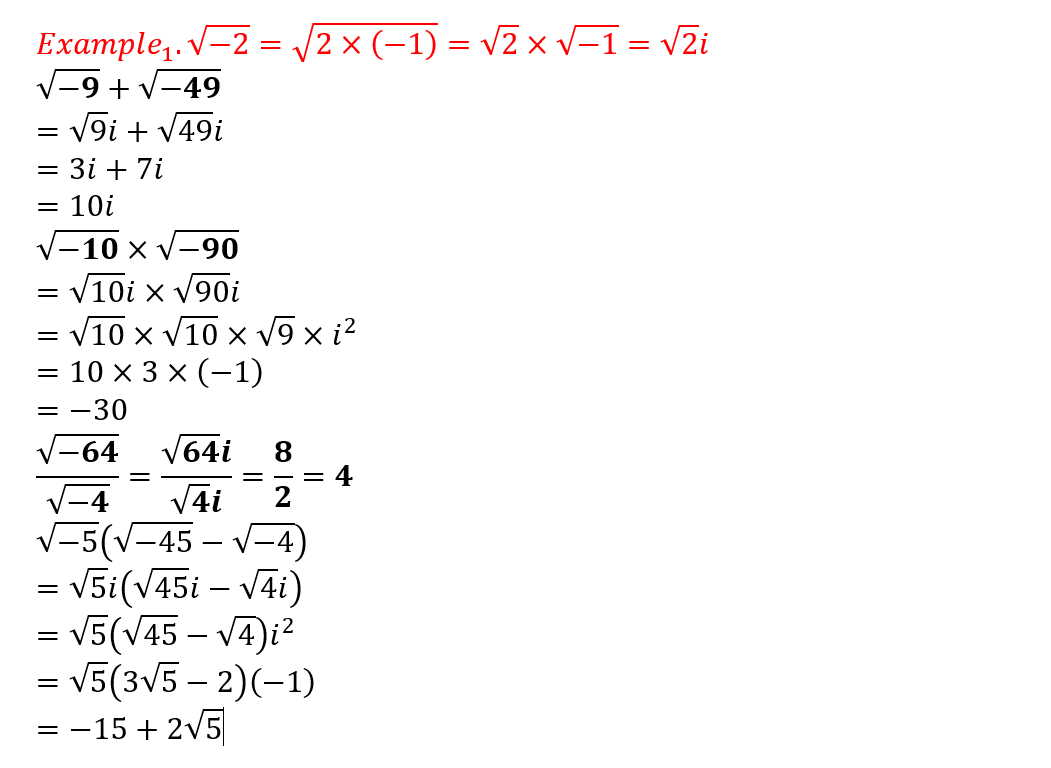Complex Numbers.
or i2=-1.
Definition
A complex number is any number that can be written as a+bi, Where i is the imaginary unit a and b are real numbers.
In your study of mathematics, you may have noticed that some quadratic equations do not have any real number solutions.
For example, try as you may, you will never be able to find a real number solution to the equation x2=-1, This is because it is impossible to square a real number and get a negative number!
However, a solution to the equation x2=-1, does exist in a new number system called the complex number system.
The backbone of this new number system is the imaginary unit, or the number i.For example, try as you may, you will never be able to find a real number solution to the equation x2=-1, This is because it is impossible to square a real number and get a negative number!
However, a solution to the equation x2=-1, does exist in a new number system called the complex number system.
or i2=-1.Example.1
A complex number is any number that can be written as a+bi, Where i is the imaginary unit a and b are real numbers.
a+bi
a is real part
b is Imaginary part
a is called the real part of the number, and b is called the imaginary part of the number.
The table below shows examples of complex numbers, with the real and imaginary parts identified. Some people find it easier to identify the real and imaginary parts if the number is written in standard form.Complex Number | Standard Form a+bi |
Description of parts |
|---|---|---|
| 3i-2 | -2+3i | The real part is -2 and Imaginary part is 3 |
| 4-7i | 4+(-7)i | The real part is 4 and Imaginary part is -7 |
| -3 | -3+0i | The real part is -3 and Imaginary part is 0 |
| 2i | 0+2i | The real part is 0 and Imaginary part is 2 |